Introduction

As I write this, there's an ongoing effort here to make Anoma and its components more formal. A purely English specification is ambiguous, at the very least, and making things more mathematically precise is essential for both understanding and implementation of Anoma. Part of this is formalization of an algorithm called Heterogeneous Paxos, a decentralized consensus algorithm intended to allow consensus to be achieved similar to Paxos without making identical assumptions about quorums.

• Heterogeneous Paxos: Technical Report by Isaac Sheff, Xinwen Wang, Robbert van Renesse, Andrew C. Myers

A formalization was made using TLA+, but we've moved to using Isabelle for greater ease in proving theorems. You can find the formalizations here:

• TLA+ Formalization
• Isabelle Formalization

One of my core goals when undertaking this project was to understand how to take a concurrent program and formalize it mathematically. In general, what does this look like? My expectation was that things would differ significantly from more usual algorithm formalizations, but, actually, it ended up not being as novel as I thought. In this post, I want to describe the general idea of formalizing concurrent programs, some different approaches, and some connections to more abstract mathematics. For this post, I will not explain HPaxos in any detail, but I will use some of its implementation in enough detail to demonstrate some broad points. You don't need to understand distributed consensus to understand this post; it's just my inspiration.

Case Study: HPaxos in TLA+ vs. Isabelle

Let's start with TLA+. This is a system designed to formalize concurrent programs. It is a first-order temporal logic. The core specification of many algorithms in TLA+, including HPaxos, will look like this

Spec == Init /\ [][Next]_vars

Here, /\ is conjunction, [] is a temporal operator, saying something like "this will always hold in the future". There are a couple of ways of thinking about this. vars is a product of variables put in global scope;

vars == << msgs, known_msgs, recent_msgs, queued_msg,
           2a_lrn_loop, processed_lrns, decision, BVal >>

These define the state of the network executing the algorithm. Init and Next are propositions that may refer to these global variables. Init just describes the starting state

Init ==
    /\ msgs = {}
    /\ known_msgs = [x \in Acceptor \cup Learner |-> {}]
    /\ recent_msgs = [a \in Acceptor \cup Learner |-> {}]
    /\ queued_msg = [a \in Acceptor |-> NoMessage]
    /\ 2a_lrn_loop = [a \in Acceptor |-> FALSE]
    /\ processed_lrns = [a \in Acceptor |-> {}]
    /\ decision = [lb \in Learner \X Ballot |-> {}]
    /\ BVal \in [Ballot -> Value]

One thing to note about this is that this isn't deterministic. Init is not a starting state, it's a description of starting states. While most of the variables are forced into a specific value, BVal is only asserted to be some function. It can be any function, Init doesn't care. As such, Init may be thought of as a predicate over states.

Next decomposes into a disjunction of options.

Next ==
    \/ ProposerSendAction
    \/ AcceptorProcessAction
    \/ LearnerAction
    \/ FakeAcceptorAction

I won't go into all of them, but let's look at that first in some detail;

ProposerSendAction ==
    \E bal \in Ballot : Send1a(bal)

Send1a(b) ==
    /\ Send([type |-> "1a", bal |-> b, ref |-> {}])
    /\ UNCHANGED << known_msgs, recent_msgs, queued_msg,
                    2a_lrn_loop, processed_lrns, decision >>
    /\ UNCHANGED BVal

Send(m) == msgs' = msgs \cup {m}

\E x \in X : Y means there exists an X, called x, such that Y.

Notice that Send is asserting a relation between the variable msgs and msgs'. This is relating variables between subsequent transition steps. There's also a bunch of UNCHANGED declarations, also relating variables between subsequent transition steps. This makes Next and its constituents a relation between states. This is significant since we don't know in what order the nodes/actors in the networks will act. As such, the most we can say is that there's a relation between state transitions; not necessarily a function computing transitions.

This relation is then modified into a predicate over histories using the modalities of the logic.

[][Next]_vars

This means that, forever into the future, Next relates any state to the next state, unless the state doesn't change at all.

TLA+ looks quite peculiar among the ecosystem of formal proving systems. The most popular systems today tend to be based on some kind of type theory, for example Agda, Lean, or Coq. Isabelle is quite different from these, being based on classical higher-order logic, but it's generally far easier to translate between it and other systems. How would one translate the TLA+ specification?

The key is to take seriously the idea that propositions in TLA+ mentioning global variables are predicates/relations over states. In Isabelle, we can write out the state as;

record State =
  msgs :: "PreMessage list"
  known_msgs_acc :: "Acceptor ⇒ PreMessage list"
  known_msgs_lrn :: "Learner ⇒ PreMessage list"
  recent_msgs :: "Acceptor ⇒ PreMessage list"
  queued_msg :: "Acceptor ⇒ PreMessage option"
  two_a_lrn_loop :: "Acceptor ⇒ bool"
  processed_lrns :: "Acceptor ⇒ Learner set"
  decision :: "Learner ⇒ Ballot ⇒ Value set"
  BVal :: "Ballot ⇒ Value"

There are some differences already. TLA+ is untyped, and so, has a separate proposition asserting well-typedness;

TypeOK ==
    /\ msgs \in SUBSET Message
    /\ known_msgs \in [Acceptor \cup Learner -> SUBSET Message]
    /\ recent_msgs \in [Acceptor \cup Learner -> SUBSET Message]
    /\ queued_msg \in [Acceptor -> Message \cup {NoMessage}]
    /\ 2a_lrn_loop \in [Acceptor -> BOOLEAN]
    /\ processed_lrns \in [Acceptor -> SUBSET Learner]
    /\ decision \in [Learner \X Ballot -> SUBSET Value]
    /\ BVal \in [Ballot -> Value]

But, nothing super interesting is happening. One may note a split between Learner and Acceptor in the Isabelle formulation, but this isn't important for this post. From here, we can define analogs of Init and Next. Since Init has only one true parameter, we can turn it into a function that returns a state.

fun Init :: "(Ballot ⇒ Value) ⇒ State" where
  "Init bval = ⦇ 
      msgs = [], 
      known_msgs_acc = (λ_. []), 
      known_msgs_lrn = (λ_. []), 
      recent_msgs = (λ_. []), 
      queued_msg = (λ_. NoMessage), 
      two_a_lrn_loop = (λ_. False), 
      processed_lrns = (λ_. {}), 
      decision = (λ_ _. {}), 
      BVal = bval 
    ⦈"

We could have also defined it as a predicate returning a bool, but it's generally better to take advantage of functional features when possible for ease of use. For Next, it really should be a relation;

fun Next :: "State ⇒ State ⇒ bool" where
  "Next st st2 = (
       ProposerSendAction st st2
     ∨ AcceptorProcessAction st st2
     ∨ LearnerAction st st2
     ∨ FakeAcceptorAction st st2
  )"

How do we express Init /\ [][Next]_vars? As I described it before, it should be a predicate about the history. What is a history? A simple answer is an infinite stream of states; that is, a function from natural numbers into states. Using that description, we'd get

fun Spec :: "(nat ⇒ State) ⇒ bool" where
  "Spec his = (
    (∃b :: Ballot ⇒ Value. his 0 = Init b) ∧
    (∀n :: nat. his n = his (1 + n) ∨ Next (his n) (his (1 + n)))
  )"

While looking quite different, this has the same meaning as the original Spec. But, now, the meanings of the modalities and global variables are made explicit.

Taking this seriously, we can translate other modal concepts into this same framework. For example, a commonly used concept is that of weak fairness, called WF in TLA+. One definition provided is in

• Safety, Liveness, and Fairness by Leslie Lamport

Any suffix of b whose states all satisfy ENABLED <<A>>_v contains an <<A>>_v step.

Here, b is our history. We can easily formulate this as

fun Enabled :: "(State ⇒ State ⇒ bool) ⇒ State ⇒ bool" where
  "Enabled r st = (∃st2. r st st2)"

fun WF :: "(State ⇒ State ⇒ bool) ⇒ (nat ⇒ State) ⇒ bool" where
  "WF p his = (
    ∀i. (∀j ≥ i. Enabled p (his j)) ⟶ (∃j ≥ i. p (his j) (his (j + 1)))
  )"

The important thing is that these formulations are far more portable than the original, modal formulas, as they can be expressed in a wider variety of systems. There's nothing essential about the way TLA+ formulates things; it's just opinionated. Although, the modal formulations exist for a reason; they are far more concise and algebraic properties become more obvious. Of course, if we want, we can define the modalities as well.

What I've written here is certainly not the only approach. Martin Kleppmann posted a blog post on the same topic here

• Verifying distributed systems with Isabelle/HOL

The main difference, as I see it, between what I present here and what Kleppmann does is how the history is formulated. Instead of constraining a stream, Kleppmann defines an inductive predicate over lists of states, where each list is a prefix of the whole history. Each state is still implicitly indexed by a natural number, being the place in the list where that state is. It's not clear to me what advantages/disadvantages this approach has over the one I presented here, but there's definitely room for exploration at this point.

Insights from Coalgebra

In a previous post, I brought up the concept of a coalgebra as useful for modeling machines of various kinds in an abstract way. I also mentioned they have a close connection to modal logics through the observation that Kripke semantics is a coalgebra.

To review, we may view a coalgebra as a generalized state transition function. Given some type of state, $S$, a coalgebra that takes an $S$ as input will return new $S$'s in a structured way. Given some kind of probability distribution over $S$, $D(S)$, a non-deterministic function of type $S \rightarrow D(S)$, sometimes called a "Markov kernel", is a $D$-coalgebra, where $D$ is the functor of the coalgebra. We can view each application of the function as a nondeterministic step. As another example, we may imagine a function that waits for an input of type $A$ during each transition. A function of the type $S→S^A$ would be an example of a $−^A$-coalgebra.

To get to the modal logics, we must ask about the final coalgebra of a functor. Given some functor $F$, we may consider the greatest-fixed-point of F,

• $G_F := \nu X . F(X) \equiv F(\nu X . F(X))$

This type will consist of infinite many layers in the shape of $F$. A term of this type represents a history for some coalgebra $S \rightarrow F(S)$. The final coalgebra is the (isomorphism) coalgebra $\text{fix} : G_F \rightarrow F(G_F)$ . What makes it final is the existence of, for any other $F$-coalgebra $c$ over the state $S$, a unique function $beh_c : S \rightarrow G_F$ identified by the coalgebra homomorphism property;

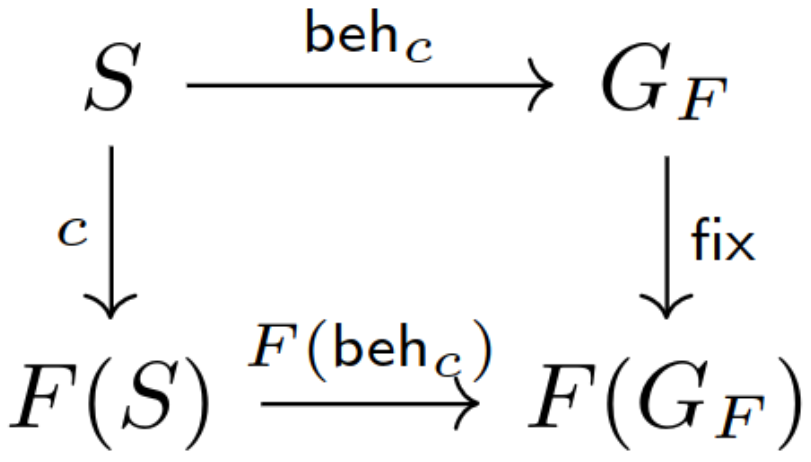
$beh_c$ will return the history of $c$, played forward from a given $S$.

The most well-known example of a greatest-fixed-point type is a stream. A stream of $A$s is the GFP of the functor

• $F(X) := A \times X$

It will have infinite many layers, each consisting of a single $A$.

At first glance, it may seem that this is the correct notion of history. However, this isn't what the theory of coalgebra would actually suggest. A coalgebra whose history is a stream will be a deterministic function of type $S \rightarrow A \times S$ that outputs an $A$ at each time step. There is a well-developed theory of such coalgebras, going under the names "stream differential equations" or "behavioral differential equations".

• Stream Differential Equations: Specification Formats and Solution Methods by HH Hansen, C Kupke, and J Rutten

The connection to differential equations is through the theory of analytic functions. A Taylor Series is a stream of coefficients defining an analytic function when it converges. From a system of differential equations, one can derive a recurrence relation which computes the coefficients of the Taylor Series representing a solution. See

• Calculus in coinductive form by Dusko Pavlovic and M. Escardó
• On the Coalgebra of Partial Differential Equations by Michele Boreale

Many core properties of differential equations still hold when generalizing to streams.

Unfortunately, concurrent programs are not deterministic. Because the agents can act in many different orders, they are not stream coalgebras. What are they? Well, we may observe that the powerset operation, $\mathcal{P}$, is a functor. We can define the functor map in Isabelle as;

fun power_map :: "('a ⇒ 'b) ⇒ ('a ⇒ bool) ⇒ 'b ⇒ bool" where
  "power_map f pa b = (∃a. pa a ∧ b = f a)"

A relation between $S$ and itself can be viewed as a function from $S$ onto $\mathcal{P}(S)$. Doing this with a relation between worlds given from a Kripke frame, we have a coalgebraic formulation of the semantics of modal logic. We can easily do this with the Next relation, treating the states as possible worlds.

The coalgebraic approach to modal logic gives us substantial generalizations of a variety of modal concepts. You can find more details in

• Introduction to Coalgebra by Bart Jacobs
• Coalgebraic semantics of modal logics: An overview by Clemens Kupke and Dirk Pattinson

While we didn't take this approach for formalizing HPaxos, it's worth consideration for future work on concurrent programs.